PHPでは、変数に 0.1 を代入すると float 型と判定されます。
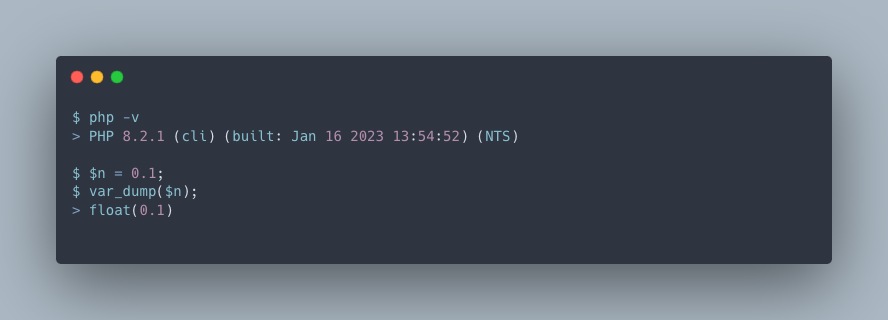
sprintf() で表示したところ小数部は53桁あり、それ以降を切り捨てる内容の警告が表示されました。
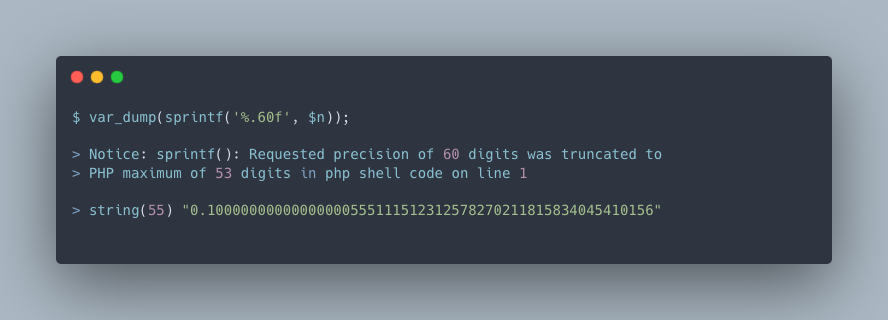
float 型の 0.1 は、なぜこのような値に変換されるのでしょうか?
浮動小数点がメモリに格納される仕組みを解説しながら理由を探ります。
10進数と2進数の表記(整数)
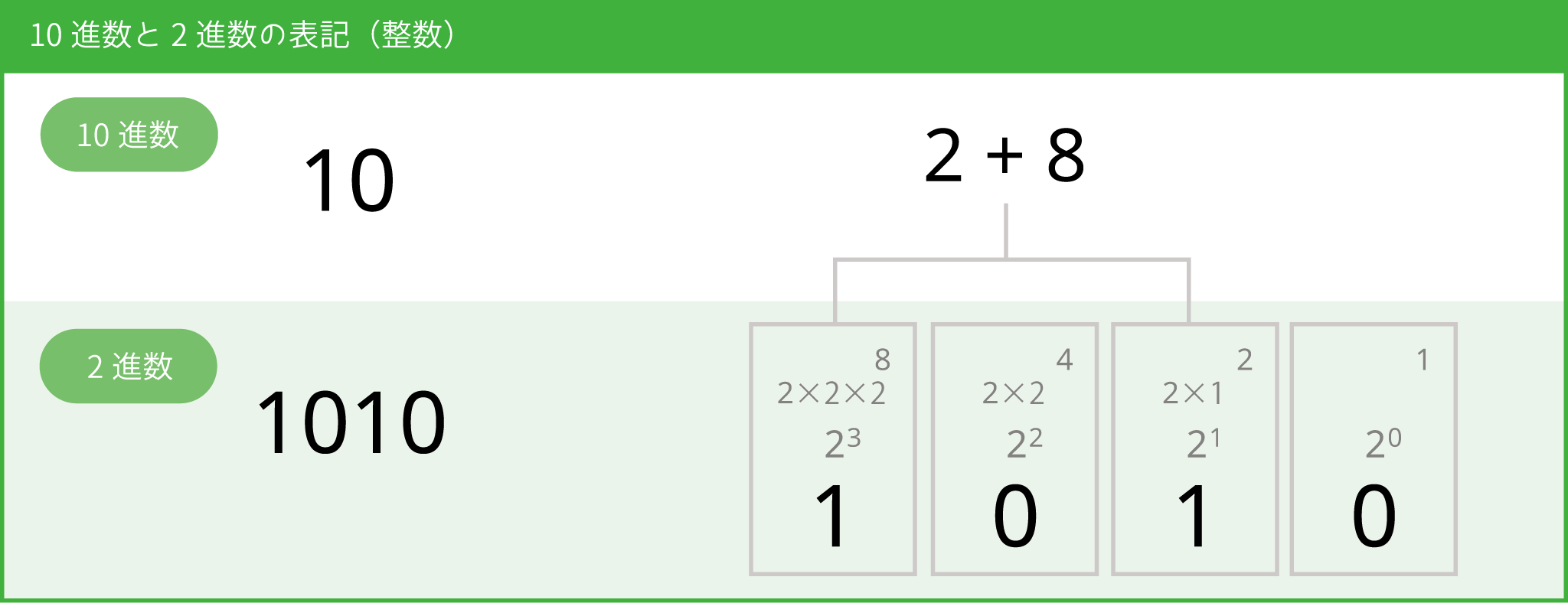
数値はメモリ上に2進数で格納されます。
2進表記の整数は 右端(一の位) から、2の0乗、2の1乗、2の2乗、2の3乗…を表します。2進数なので、格納される値は「0」または「1」の二通りです。「0」または「1」が格納される領域を「ビット」と呼びます。
10進数の 10 は2進数では 1010 です。「1」が格納されたビット(2の1乗と、2の3乗)の合計(2 + 8)が10進表記になります。
10進数と2進数の表記(小数)
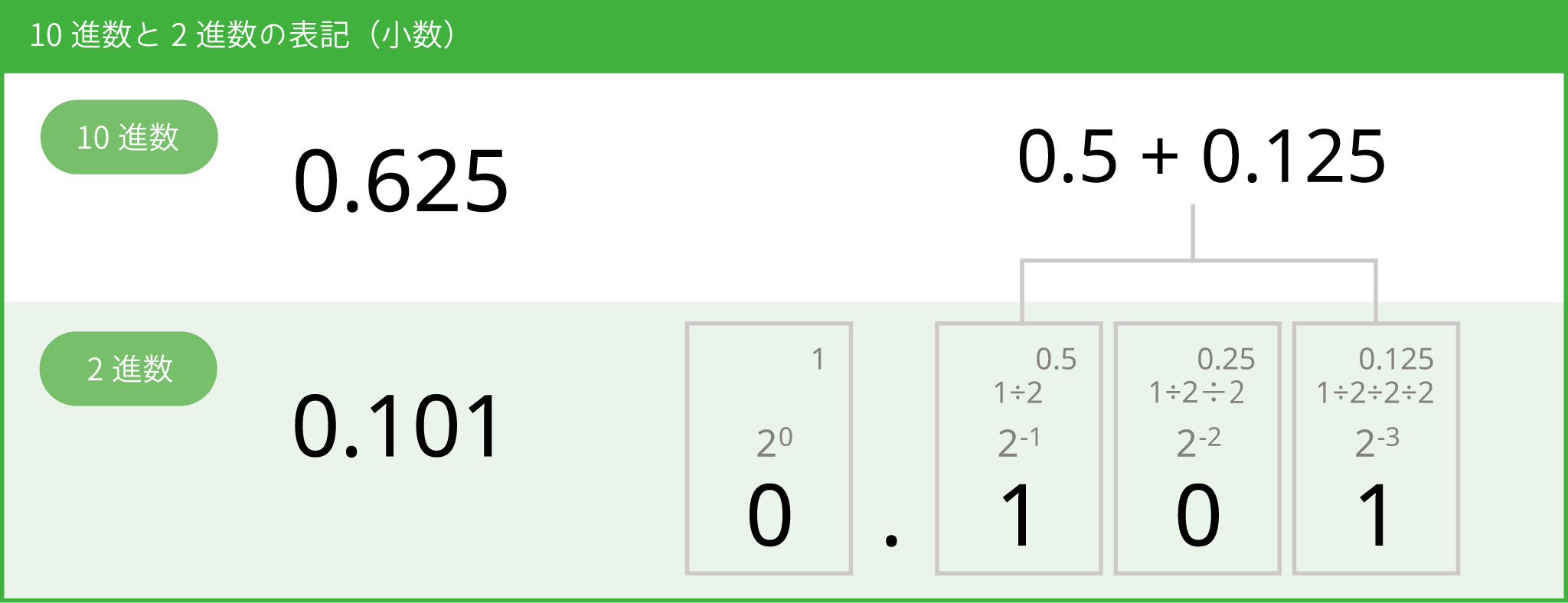
2進表記の小数は 左端(小数第一位) から、2の-1乗、2の-2乗、2の-3乗…を表します。マイナスのn乗は割り算で求めます。2のマイナス3乗は、1に対して「÷2」を3回くりかえした数です。
10進数の 0.625 は2進数では 0.101 です。「1」が格納されたビット(2の-1乗と、2の-3乗)の合計(0.5 + 0.125)が10進表記になります。
10進数から2進数の変換(整数)

10進数の 22 は2進数では 1 0110 です(読みやすいよう4桁で区切っています)。
- 対象の10進数をひたすら2で割り算します
- 割り算の結果が0か1になればそこで終了します
- 余りの数を計算の新しい順に並べたものが、2進数の表記です
10進数から2進数の変換(小数)

10進数の 0.1 は2進数では 0.0001 1001 1001 1001... です。
- 対象の10進数の小数部分を取り出し、ひたすら2で掛け算します
- 次の計算に進む時も同じように小数部分を取り出します
- 結果の整数部分を計算の古い順に並べたものが、2進数の表記です
0.1 の2進表記を求めた時、結果が1.6になるとそこから同じ計算をぐるぐる循環してしまいます。このように小数で同じ数字の並びが無限に繰り返されることを「循環小数」と呼びます。

循環小数である 0.0001 1001 1001 1001... は、有限のメモリ上に正確な値を格納することができません。小数の割り当てが4ビットだと 0.0001 、8ビットだと 0.0001 1001 というように、たくさんのビットを確保すればそれだけ詳細な表現ができるため誤差は少なくなります。このことを「精度」と呼びます。
浮動小数点のフォーマット
浮動小数点の標準は IEEE 754 で規定されます。数種類のフォーマットのうち、使用ビットが多いものほど高い精度を実現します。
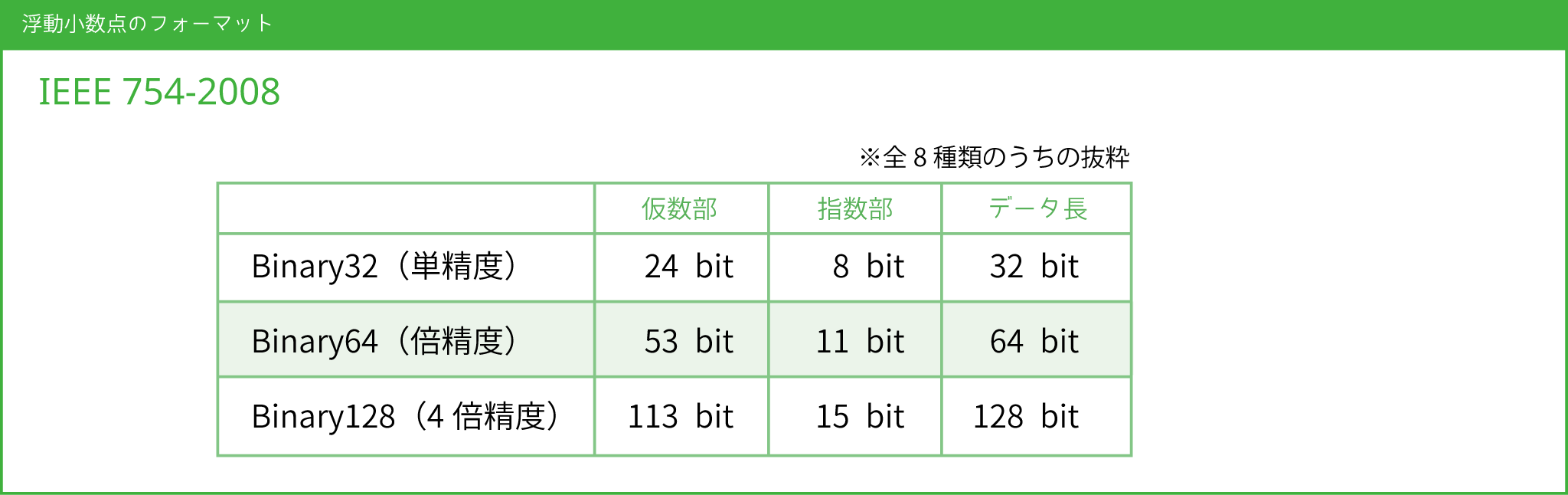
ドキュメントを見ると、PHPの浮動小数点は IEEE 754 の Binary64(倍精度) であることが分かります。
浮動小数点数の精度は有限です。
システムに依存しますが、PHP は通常 IEEE 754 倍精度フォーマットを使います。浮動小数点数 | PHPマニュアル
https://www.php.net/manual/ja/language.types.float.php
仮数部

仮数部は整数の一の位を「1」として格納するルールがあります。
0.0001 1001 1001 1001… の小数点を4回移動すると 1.1001 1001 1001… になります。この結果から 1. を除いた部分が「仮数部」に格納されます。
1001 1001 1001… という循環小数のように仮数部のビットに収まらない場合、丸め処理が行われます。
指数部

小数点を移動した回数に 1023 を足した数が「指数部」に格納されます。この数は「バイアス」と呼び、精度ごとに規定されています。今回の例の Binary64(倍精度) の場合 1023 になります。
小数点の移動回数はマイナスで表します。今回は4回移動したので 1023 + (-4) で 1019 が格納されます。
符号部

仮数部、符号部の他に、プラスマイナスを表す「符号部」があります。符号部は0なら正、1なら負を表します。
浮動小数点の取り出し
浮動小数点を10進数に変換する時は「仮数部」「指数部」「符号部」に格納された値から計算されます。この時、仮数部が丸められていると元の値に戻すことはできません。

sprintf('%.53f', $n) してみると、丸めが発生する 0.1 や 0.2 は Binary64(倍精度) の精度いっぱいまで桁を持ち、 0.5 のように2の-n乗で表現できるものは丸めが発生しないことが分かります。

まとめ
精度の高い浮動小数点は、人間が読みやすいように表示されるため、正確な値であるかのように見えます。

内部的には2進数への変換と丸め処理により、わずかな誤差が発生することがあります。var_dump() による警告は、浮動小数点の表現の限界を示したものと言えます。

以上です。
float 型の理解の一助になれば幸いです。